新型コロナウイルス感染者数のグラフがベル型曲線になるのはナゼ 〜感染者減少の仮説〜
最近、毎日のニュースで新型コロナ感染者数のグラフを見ますが、きれいなベル型の曲線を描いて増減しています。国、地域、ウイルス株が違っても大体同じ形になることが多い...
この現象は、感染症数理モデルを使ったシミュレーションでうまく説明できます。モデルには様々なものが提唱されていますが、その原型となるものは、W・O・カーマックとA・G・マッケンドリックの1927年の論文で提案されたもので、「SIRモデル」と呼ばれるものです。
SIRモデル
❝ SIR数理モデルは、新型の感染症のため免疫を持つ人はいないこと、外部の都市との間で人口移動がないこと、人口は密集し不特定多数の人との接触があること、ペストのような急速かつ短期的な流行を想定したモデル方程式で、集団を以下の3つに分類し、各集団の人数を微分方程式で表します。
- 未感染者(Susceptable)
- 感染者(Infected)
- 感染後死亡もしくは回復による免疫を獲得した者(Recovered)
出典:感染症流行を予測する数理モデル SIR|微分方程式によるシミュレーション
この微分方程式を使ってコンピュータシミュレーションを行うことで感染の状況を見ることが出来ます。微分方程式の数値解法はいろいろありますが、簡易的にエクセルだけで行うことも出来ます。
❝第t週(ここでは週ごとにした)におけるS、I、Rの人数をそれぞれS(t)、I(t)、R(t)とする。(1)式は感染症への免疫がない人のt週からt+1週への増減を示す。
S(t+1) - S(t) = -b × S(t)/S(0) × I(t)・・・(1)
次に、(2)式はt週からt+1週にかけて感染から回復した人々の数を示す。
R(t+1) - R(t) = I(t) × c・・・(2)
(3)式はt週からt+1週への感染者数の増減を示す。
I(t+1) - I(t) = b × S(t)/S(0) - I(t) × c・・・(3)
出典:感染症についてSIRモデルから学んだこと❞
人口1億人で、第1週に1人が感染したとすると以下のようなエクセルの計算式になります。
計算結果から、1週間の新規感染者数、未感染者数(S)、感染者数(I)、感染経験者数(R)をグラフにすると以下のようになります。
 |
| 図2 感染症流行のシミュレーション |
グラフから新規感染者数(棒グラフ)の推移がベル型曲線になることが分かりました。しかしこのモデルでは最終的に感染者の総数が全人口1億人近くになってしまうので実際の感染状況とは大分違います。そこで、モデルを少し改良してみました。
感染対策の効果
集団の多くが十分な感染対策をしているが、一部(全人口の1%:100万人)の人が対策不十分な場合を考えてみます。十分な感染対策をしている集団とそうでない集団の2つに分け、1人から何人に感染するかという再生産数を次のように設定します。- 感染対策不十分な人同士:1.5
- 感染対策不十分な人から感染対策している人へ:1.05
- 感染対策している人同士:0.3
- 感染対策している人から感染対策不十分な人へ:0 (計算対象外)
感染対策している人9900万人、感染対策不十分な人100万人とし第1週に対策不十分な人1人が感染したとして同じようにエクセルで計算しました。1週間の新規感染者数のグラフは以下のようになります。
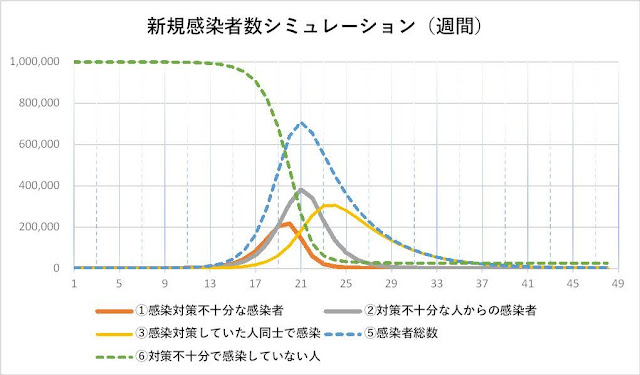 |
| 図3 新規感染者数シミュレーション |
このモデルでは13週くらいから対策不十分な人 (①)の中での感染増加(1000人超え)が始まり、同時に感染対策不十分な人から対策している人(②)への感染も増加していきます。そこから2週間ほど遅れて感染対策している人同士(③)の感染が増加します。20週で感染対策不十分な人(①)の感染ピークを迎え、1週間遅れて全体の感染者数(⑤)がピークとなり減少していきます。しかし、その後も感染対策している人同士(③)の感染は増え続け、さらに3週間過ぎてピークとなり減少していきます。最終的には全人口の約6%(約600万人)が感染して終息します。
ここで注目したいのは、2つのグループ(十分な感染対策をしている集団とそうでない集団)の感染拡大速度に差があるため、それぞれの感染者数、全体の感染者数のピークがズレるという点です。全感染者数(⑤)が最大となる21週には、対策不十分な人(①)の感染ピークは過ぎていて、主要な感染拡大源となる「対策不十分だが感染していない人の数(⑥)」が4分の1まで減っています。
感染者数の減少
このモデルでの感染推移を新規感染者の中で感染対策をしている人と不十分な人の割合を別の観点からグラフにしてみます。
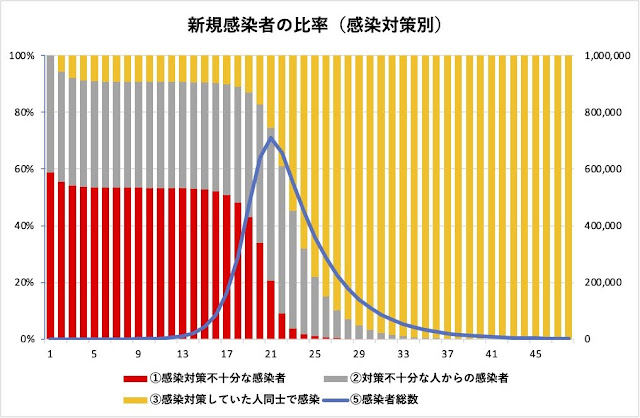 |
| 図4 新規感染者の比率 |
曲線(⑤)が一週間の新規感染者数の総数を表し、棒グラフはその週の総数を100%としたときの感染対策別の割合となります。感染者数のピークとなる21週では、感染対策不十分な感染者(①)の比率が2割程度まで減っており、感染者の大部分が感染対策をしていた人になっています。
この時点で感染症の専門家が状況分析すれば、「感染拡大の原因となる対策不十分な感染者が大幅に減っているので感染の終息が近い」と判断すると思われます。一方で多くの国民は「感染者数が急速に増えている。しかも感染対策していない人が減って、対策していても感染した人が増えている。このままでは感染拡大を止められない。」と考えるかもしれません。これは1つのモデルの話ですが、日本の第5波でも似たような傾向の報道がなされていたように思います。この時点で専門家が終息が近いと言っても信じる人は多くないでしょうし、仮に信じられたとしても対策がゆるむと再拡大の危険があるので、慎重な言い回しになるのは仕方ない事かもしれません。
有効な感染対策
このモデルでのシミュレーションから、多くの国民が有効な対策をしていれば感染拡大を抑え込めるという事が推察されます。そして日本の第5波が、このモデルに似た状況になっていたように見えます。
それでは、有効な感染対策は何かということを考えると、今更ですが、
- マスク着用、手指消毒
- 密を避ける
- 換気
- 黙食
- ワクチン接種
恐らく、この中の1つ、2つだけでは十分な効果がなく、全部実行することが必要になるでしょう。
今の状況が続けば、徐々に制限を緩和する方向に進めそうですが、新たな変異株が入って来れば状況が一変する可能性があります。現時点で有効と考えられている方法が利かないかもしれません。その時、次の一手があるのかが気がかりです。





